

Answer: D
Solution:
Let x be the number of hours she must work for the final week. We are looking for the average, so (8+11+7+12+10+x)/6=10. Solving gives x=12.
中文解析:
按照计划必须工作:10*6=60小时。已经工作了8+11+7+12+10=48小时, 还需要工作60-48=12小时。答案是D。

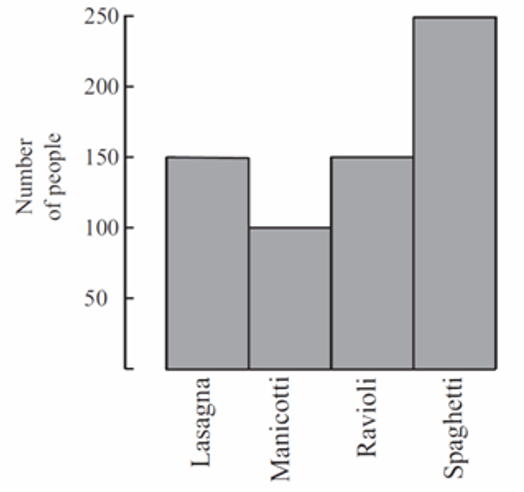
Answer: E
Solution:
250/100=5/2.
中文解析:
喜欢Spaghetti的有250人, 喜欢manicotti的有100人。两者的比值是:250/100=5/2.
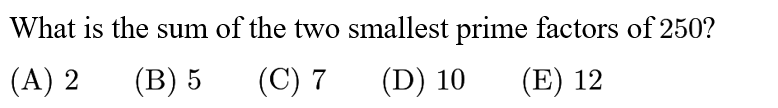
Answer: C
Solution:
The smallest two prime factors of 250 are 2 and 5. 2+5=7.
中文解析:
画出prime factor tree, 可以看出250的prime factor有:2和5. 最小的也是2和5,其和是2+5=7. 答案是C。

Answer: D
Solution:
Georgie can enter the haunted house through any of the six windows. Then, he can leave through any of the remaining five windows. So, Georgie has a total of 6*5=30 ways he can enter the house by one window and leave by a different window.
中文解析:
进入的时候从6个窗户中选择一个, 出去的时候从剩下的5个窗户中选择一个,共有:6*5=30种选择。

Answer: B
Solution:
Let x be the number of weeks. Thus, we have the equation 50+35+15+16*x=500. Thus x=25.
中文解析:
他的生日能得到的钱数是:50+35+15=100元, 为了买500元的山地自行车,还需要400元。他每周能挣到16元,需要工作400/16=25周。答案是B。

Answer: E
Solution:
The percent decrease is (the amount of decrease)/(original amount) 。the amount of decrease is 41-7=34. so the percent decrease is 34/41=80%.
中文解析:
长途电话费从41降到了7,降幅是34. 相比最初的41,降低的百分比是:34/41=0.8. 即80%。答案是E。

Answer: D
Solution:
Let x be the average of the remaining 4 people. The equation we get is (4x+18)/5=30. Thus, x=33.
中文解析:
5个人的总年龄是5*30=150. 一个18岁的人离开后,总年龄是150-18=132. 剩下的4个人的平均年龄是132/4=33岁。答案是D。

Answer: B
Solution:
We know that ABED is a square with side length 3. We subtract DC and DE to get the length of EC. EC=6-3=3. We are trying to find the area of triangle BEC. So, 1/2 * 3*3=4.5.
中文解析:
BE=AD=3;EC=DC-DE=6-3=3. 在直角三角形BEC中,两条直角边都是3, 面积是3*3/2=4.5. 答案是B。

Answer: B
Solution:
The number in the first row, last column must be a 3 due to the fact if a 3 was in the first row, second column, there would be two threes in that column. By the same reasoning, the number in the second row, last column has to be a 1. Therefore the number in the lower right-hand square is 2.
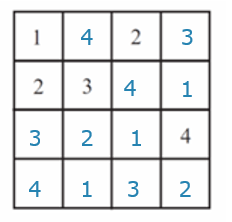
中文解析:
如图所示,右下角应该填2. 答案是B。
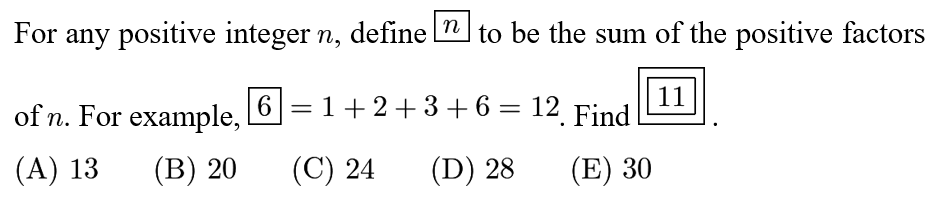
Answer: D
Solution:
Special symbol of 11 =1+11=12;special symbol of 12=1+2+3+4+6+12=28.
中文解析:
11的因子是1和11. 因此11的框是1+11=12. 12的因子有:1,2,3,4,6,12. 因此12的框是: 1+2+3+4+6+12=28. 答案是D。
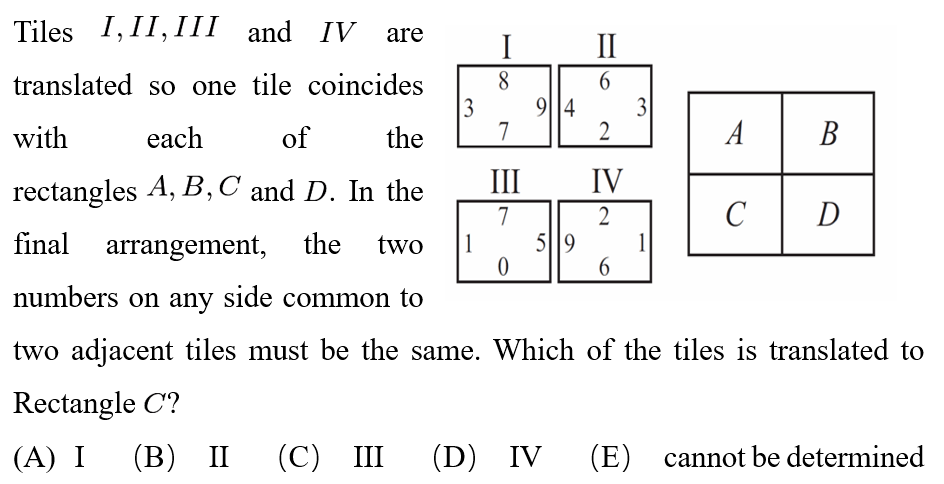
Answer: D
Solution:
We first notice that tile III has a 0 on the bottom and a 5 on the right side. Since no other tile has a 0 or a 5, Tile III must be in rectangle D. Tile III also has a 1 on the left, so Tile IV must be in Rectangle C. The answer is D .
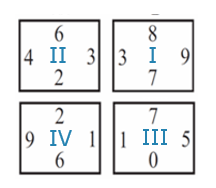
中文解析:
如上图所示,放在C位置的应该是IV。答案是D。

Answer: A
Solution:
The six equilateral triangular extensions fit perfectly into the hexagon meaning the answer is 1:1.
中文解析:
六边形可以从中心划分成边长为1的6个正三角形组成。六角星的突出的6个角也是边长为1的6个正三角形。因此面积的比值是1:1. 答案是A。

Answer: C
Solution:
Let x be the number of elements in A and B. Since the union is the sum of all elements in A and B, and A and B have the same number of elements then, 2x-1001=2007, thus x=1504.
中文解析:
集合A和几何B的元素个数相同, 假设都是x. 则x+x-1001=2007. 求得x=1504. 即集合A中有104个元素。答案是C。

Answer: C
Solution:
The area of a triangle is shown by 1/2 *b*h. We set the base equal to 24, and the area equal to 60, and we get the height, or altitude, of the triangle to be 5. In this isosceles triangle, the height bisects the base, so by using the Pythagorean Theorem, a*a+b*b=c*c, we can solve for one of the legs of the triangle (it will be the hypotenuse, c). a=12, b=5, c=13. The answer is 13.
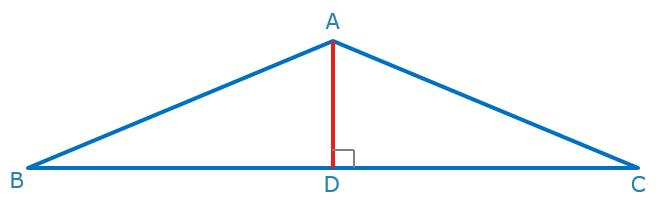
中文解析:
如上图所示的等腰三角形ABC中, AD垂直于BC,是三角形的高。三角形ADC的面积是三角形ABC的一半,即30. 在直角三角形ADC中,底是24/2=12, 根据三角形面积公式,可求得高AD是30*2/12=5. 在直角三角形ADC中,两条直角边分别是5和12, 根据勾股定理,其斜边是13. 即等腰三角形ABC的那两条相等的边的长度是13. 答案是C。
Answer: A
Solution:
According to the given rules, every number needs to be positive. Since c is always greater than b, adding a positive number (a) to c will always make it greater than b.Therefore, the answer is A.
中文解析:
a,b,c都是正数, c大于b, c+a更大于b. 因此选项A不可能。答案是A。

Answer: A
Solution:
The circumference of a circle is obtained by simply multiplying the radius by 2*Pi. So, the C-coordinate (in this case, it is the x-coordinate) will increase at a steady rate. The area, however, is obtained by squaring the radius and multiplying it by Pi. Since squares do not increase in an evenly spaced arithmetic sequence, the increase in the A-coordinates ( y- coordinates) will be much more significant. The answer is A.
中文解析:
半径为1的圆,周长是2Pi, 面积是1Pi; 半径为2的圆,周长是4Pi,面积是4Pi;半径为3的圆,周长是6Pi, 面积是9Pi,半径是4的圆,周长是8Pi,面积是16Pi;半径是5的圆,周长是10Pi, 面积是25Pi. 随着周长的变化:2,4,6,8,10,面积的变化:1,4,9,16,25. 这不是线性变化,能体现这个变化规律的只有A。答案是A。

Answer: C
Solution:
Since 30% of the original 30 liters of paint was yellow, and 5 liters of yellow paint were added to make the new mixture, there are 30*30%+5=14 liters of yellow tint in the new mixture. Since only 5 liters of paint were added to the original 30, there are a total of 35 liters of paint in the new mixture. This gives 14/35=40% of yellow tint in the new mixture.
中文解析:
原来30升,黄色是9升,又加入5升黄色颜料后,黄色颜料共有14升。混合物共30+5=35升。黄色占比是14/35=40%。答案是C。

Answer: D
Solution:
We can first make a small example to find out A and B. So, 303*505=153015. The ones digit plus thousands digit is 5+3=8.
中文解析:
用小些的数字303*505=153015. 千位数是3,个位数是5, 再大些的数去相乘时,并不影响乘积的千位数和个位数。5+3=8. 答案是D。

Answer: C
Solution:
Let the smaller of the two numbers be x. Then, the problem states that (x+1)+x<100; (x+1)*(x+1)-x*x=x*x+2x+1-x*x=2x+1. 2x+1 is obviously odd, so only answer choices C and E need to be considered. 2x+1=131 refutes the fact that 2x+1<100. So the answer is 79.
中文解析:
假设这两个连续的整数分别是x和x+1, 其平方分别是x*x和(x+)*(x+)。平方差是:(x+1)*(x+1)-x*x=2x+1. 即是一个奇数。选项中只有79和131是奇数。另外,题目告知这两个连续的整数其和小于100, 则x应该小于50, 则平方差2x+1应该小于100, 只有选项79适合。答案是C。

Answer: A
Solution:
At the beginning of the problem, the Unicorns had played x games and they had won 0.45*x of these games. Next, the Unicorns win 6 more games and lose 2 more, for a total of 6+2=8 games played during district play. We are told that they end the season having won half of their games, or 0.5 of their games. We can write an equation: (0.45x+6)/(x+8)=0.5. thus x=40. Since the problem asks for the total number of games, we add on the last 8 games to get the solution 48.
中文解析:
假设在district 比赛之前,进行了x场比赛,则得胜的数量是0.45x场。又比赛了6+2场,其中6场得胜,合计赢了一半的比赛,则:(0.45x+6)*2=x+8. 可以求得x=40. 总共进行的比赛场次是40+8=48. 答案是A。
Answer: D
Solution:
There are 4 ways of choosing a winning pair of the same letter, and 2*C(4,2)=2*6=12 ways to choose a pair of the same color. There's a total of C(8,2)=28 ways to choose a pair, so the probability is (4+12)/28=4/7.
中文解析:
第一张牌任意发一张。如果同色,有3张牌同色,如果同样的字母,有一张同字母的牌。第二张牌选择这3张同色的或1张同字母的都可以,共4个选择。 第二张牌从剩余的7张牌中,如果选中这4张中的任意一张,即可获胜。 因此概率是4/7. 答案是D。

Answer: C
Solution:
Note that from any point in the square, the average distance from one side to the other is half of the side length of the square.

中文解析:
如上图所示,lemming的位置距离四条边界的距离如虚线所示。 距左边和右边的距离之和是10米,距离上面和下面的距离的和是10米。 因此距离四边的距离的平均值是: (10+10)/2=5. 答案是C。
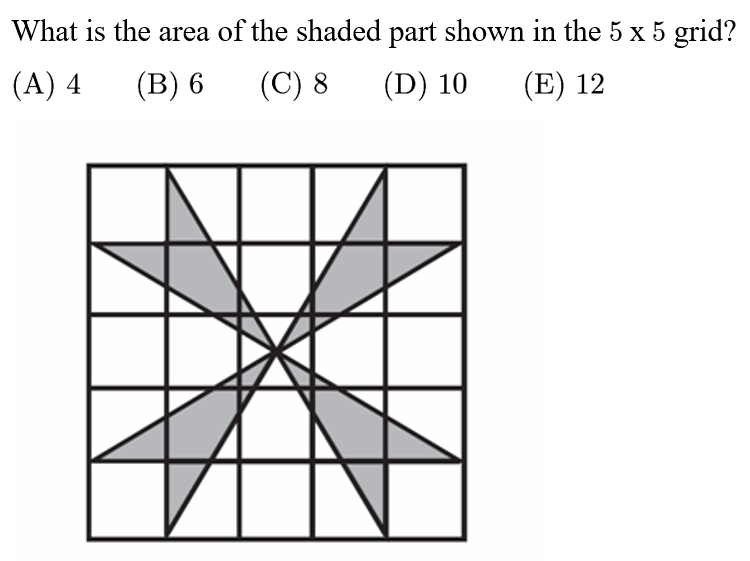
Answer: B
Solution:
The area of the square around the pinwheel is 25. The area of the pinwheel is equal to the square -the white space. Each of the four triangles have a base of 3 units and a height of 2.5 units, and so their combined area is 15 units squared. Then the unshaded space consists of the four triangles with total area of 15, and there are four white corner squares. Therefore the area of the pinwheel is 25-15-4=6.
中文解析:
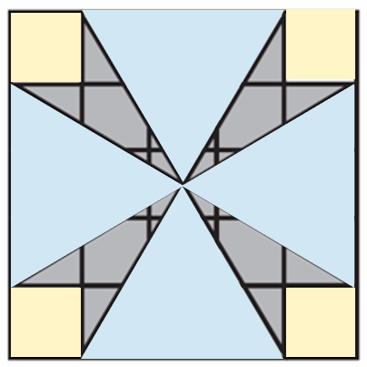
如上图所示,阴影部分的面积等于大正方形的面积减去四个浅蓝色三角形的面积,减去四个黄色小正方形的面积。
从图中可以看出,三角形的底是3,高是2.5,因此三角形的面积是3.75. 因此阴影部分的面积为:5*5-4*3.75-4*1=6。答案是B。

Answer: C
Solution:
The combination of digits that give multiples of 3 are (1,2,3) and (2,3,4). The number of ways to choose three digits out of four is 4. Therefore, the probability is 1/2.
中文解析:
从1,2,3,4 中选择3个数字,其和是3的倍数,可以选择1,2,3 或者2,3,4. 由1,2,3 组成3位数,可以有3*2*1=6中不同的排列。由2,3,4三个数字组成的3位数有3*2*1=6种不同的排列,合计6+6=12种。从1,2,3,4种选出3个数字组成3位数,共有4*3*2=24种排列。因此组成的3位数是3的倍数的概率是:12/24=1/2. 答案是C。
Answer: B
Solution:
To get an odd sum, we must add an even number and an odd number. The area of each smaller section is 1/3 * Pi*3*3=3Pi, The larger sections trisect a "ring" which is the difference of two circles, one with radius 3, the other radius 6. So, the area of the ring (annulus) is 1/3 * Pi*6*6 -3Pi=9Pi. One smaller section and two larger sections contain an odd number (that is, 1). So the probability of throwing an odd number is 3Pi+2*9Pi=21Pi. Since the area of the whole circle is 36Pi, the probability of getting an odd is 21Pi/36Pi=7/12.
中文解析:
小圆扇形的面积是:(Pi*3*3)/3=3Pi;大圆的面积是36Pi. 大圆环的1/3的面积是:(Pi*6*6-Pi*3*3)/3=9Pi. 因此飞镖射中区域“1” 的概率是:(9Pi+9Pi +3Pi)/36Pi=7/12;飞镖射中区域“2”的概率是:(3Pi+3Pi+9Pi)/36Pi=5/12. 如果两次飞镖射中的分数之和是奇数,则必须一个是1分,1个是2分。因此概率是:7/12 * 5/12 +7/12 * 5/12=35/72. 答案是B。
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,